This is the first of a three posts covering trees and using them to partition space. Each post will contain an interactive demo (bottom of the page.) This post will cover Quadtrees, followed by Octrees and k-d trees.
A Quadtree is a useful tool when one needs to store and search for points in 2d space. In a quadtree a node is either a leaf or parent with four children. 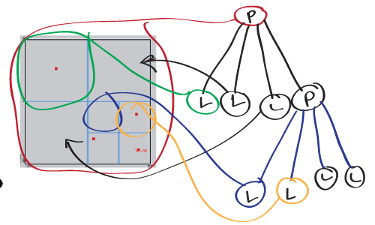
Node composition:
The example to the right shows a Quadtree with a root node, one parent node and 7 children. When using them to divide space we can see the root node in red has four children. The spaces they represent are show with the bisecting blue lines. Three of these four children are leafs, with only one of these leafs containing a data point. The child representing the SE region is not a leaf node, it is a parent and has four leafs. Two of it’s child leaf areas are shown by the blue and yellow lines. Of these leafs, three have data points. In a quadtree a node can have only two forms; a parent with four leafs or a leaf with no children. A leaf does not always contain a data point, it can represent an area with no data.
A node must contain the following:
It’s four children (if they exist) North West, North East, South East, South West regions.
A field to store its data point (X,Y)
And a struct,class or fields to store its bounding box (the area it contains usually represented as X,Y coordinates)
Optionally you can include a reference to it’s parent
Here is the class from the interactive example.
|
1 2 3 4 5 6 7 |
public class QTNode { public QTNode ParentNode; public QTNode NW, NE, SE, SW; public Coordinates LeafDataPoint; public bool UseLeafBool; public QuadTree.BoundingBox BoundingBox; } |
Point insertion:
Inserting a point is done recursively. First check if the point falls within the root nodes boundary box. The steps following are duplicated until it is placed, starting at the Root node.
Does this node have children;
-
- Yes – find the child region this point falls into and send it to the node. [side note to find the area we use the bounding box each node has. My bounding box holds three things a nodes center X, Y and it’s length. If a points X is greater than this nodes X center it falls in the East region, if it is greater than the Y center it falls to the North region. I had 01 represent NW, 11 NE, 10 SE, 00 SW.]
- No – does this node contain a data point yet?
- Yes – Make this node a parent, create its four children and pass the new point and this nodes previous data point to the new children who will use this recursive process to place
- No – store this point on this leaf.
Finding the closest data point :
Now that points are stored, one of the useful ways to use a quad tree is searching for points within an area, or finding the point closest to a coordinate without comparing the distance of every point within a tree. The logic below covers finding the closest point to a location. It can also be used to find every point within an area.
This search uses the following three objects
AlreadySearched – Hash set of already searched nodes
FoundLeafNodes – Queue to hold the nodes to check distance on [optional]
SearchBoundingBox – The BB area we need to search
SearchPoint – the X,Y coordinates we are trying to find the closest data point to
ClosestNode – the closest node found
- Step 1 recursively dive to the lowest leaf whose bounding box contains the Search Point
- Check if this leaf contain a datapoint
- Yes – Store this node as our ClosestNode and find the length from this point to our SearchPoint (node, add this node to the ClosedSet.) Construct a SearchBoundingBox centered at the Search Point with this length. We will use this to test if any other leafs contain points within this box that are closer. A box will cover some areas that do not need searched, it is however simpler and faster than a circle.
- No – go to this leafs parent, one of its descendants will contain a leaf with data. Recursively breadth search every node downward and store them in the FoundLeafNodes queue (also store every node we visit in our ClosedNode hash set) [Note the FoundLeaf queue can be eliminated by tracking the best result and testing as leafs are reached.]
- Take the queue of found points and search through them to locate the closest node. Take the length of this node and use it’s length to construct a bounding box from the center of our SearchPoint
- Now visit every node within our SearchBoundingBox to confirm we have the closest datapoint. We can check this with a simple bool test : (Mathf.Abs(BoxA.BisectX – BoxB.BisectX) * 2 < (BoxA.Length + BoxB.Length)) && (Mathf.Abs(BoxA.BisectY – BoxB.BisectY) * 2 < (BoxA.Length + BoxB.Length)). Starting at the root node recursively build the FoundLeafNodes queue.
- This node is not in our AlreadySearched set and overlaps the SearchBoundingBox
- Yes (add it to the AlreadySearched set)
- Is this a leaf node
- Yes
- If it contains data add it to the FoundLeafNodes queue
- No
- Repeat the test for all this nodes children
- Yes
- Is this a leaf node
- No
- We have already searched this node, ignore it and it’s children
- Yes (add it to the AlreadySearched set)
- Once the recursive search finishes and all the valid leafs have been added to the FoundLeafNodes queue, test all these points to find the closest node, and return it. (Don’t forget about the ClosestNode we used to construct our bounding box, it could be the closest.)
- This node is not in our AlreadySearched set and overlaps the SearchBoundingBox
Interactive Example (please note takes about 30 seconds to load):
When using the interactive example below to search for a node, that the green box represents the SearchBoundingBox used to test for the closest node. You can see how this is needed as diving down to the node which contains our SearchPoint will not always return the closest result.